| Alex_Arahort | Дата: Воскресенье, 06.05.2012, 17:46 | Сообщение # 1 |
 Admin
Группа: Администраторы
Сообщений: 91
Статус: Offline
| http://festival.1september.ru/articles/507571/
Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов.
Даже если некоторые тонкие понятия математического анализа появились вне связи с теорией рядов, они немедленно применялись к рядам, которые служили как бы инструментом для испытания значимости этих понятий. Такое положение сохраняется и сейчас.
Выражение вида
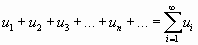
где ;;;…;;… - члены ряда; - n-ый или общий член ряда, называется бесконечным рядом (рядом).
Если члены ряда :
числа, то ряд называется числовым;
числа одного знака, то ряд называется знакопостоянным;
числа разных знаков, то ряд называется знакопеременным;
положительные числа, то ряд называется знакоположительным;
числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
функции, то ряд называется функциональным;
степени, то ряд называется степенным;
тригонометрические функции, то ряд называется тригонометрическим.
Числовым рядом называется сумма вида
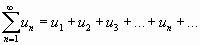
где ,,,…,,…, называемые членами ряда, образуют бесконечную последовательность; членназывается общим членом ряда.
Суммы
…………..
,
составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм .
Если при бесконечном возрастании номера n частичная сумма ряда стремится к пределу, то ряд называется сходящимся, а число - суммой сходящегося ряда, т.е.
Если частичная сумма ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к или ), то такой ряд называется расходящимся.
Если ряд сходящийся, то значение при достаточно большом n является приближенным выражением суммы ряда S.
Разность называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е., и наоборот, если остаток стремится к нулю, то ряд сходится.
Я рождён на границе меж светом и тьмой, был распят за безумные игры с судьбой...
|
| |
|
|


















